Phylogenetic inference
Coordinator/contact:
This email address is being protected from spambots. You need JavaScript enabled to view it.
This email address is being protected from spambots. You need JavaScript enabled to view it.
Introduction
Phylogenetic inference represents one of the most outstanding research topics in bioinformatics. By processing molecular sequences from modern organisms, phylogenetic methods aim to infer ancestor-descendant relationships among species and describe a hypothesis about their evolutionary history. Phylogenetic reconstruction is usually conducted according to some optimality criteria which define the overall quality of the inferred phylogenies, such as maximum parsimony and maximum likelihood. In order to tackle such problem, we must take into account two keys issues:
- Firstly, the inference of phylogenetic trees is a well-known NP-hard problem, due to the exponential growth of the tree search space as we increase the number of species under review.
- Secondly, different optimality criteria often lead to conflicting evolutionary histories for the same biological data. The choice of optimality criteria represents one of the main problems that biologists must address to process their biological sequences.
The development of new algorithmic designs based on soft computing and hardware architecture represents useful tools to resolve such kind of problems. On the one hand, we can propose new designs to infer phylogenetic trees on data sets with hundreds and thousands of species by using high performance computing. On the other hand, incongruence in phylogenetics can be addressed by defining phylogenetic inference as a Multiobjective Optimization Problem (MOP). In this research, we aim to develop new software solutions which combine multiobjective optimization, bioinspired computation, and parallelism to carry out phylogenetic analyses.
Phylogenetic Inference Problem
Phylogenetic procedures take as input an alignment composed by N molecular sequences, characterized by M sites. According to the nature of the input data, phylogenetic methods can be classified into two categories: character-based methods and distance-based methods. While character methods are defined to reconstruct evolutionary histories by processing directly the input alignment, distance methods compute a matrix of genetic distances by analyzing the diversity observed at molecular level. Distance matrices are then used to build phylogenies by using clustering algorithms. Figure 1 shows an example of these methodologies.
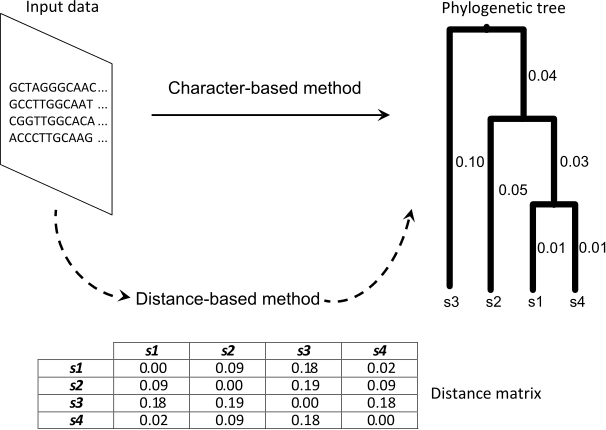
Figure 1: Phylogenetic inference
The results of applying phylogenetic methods are tree-shaped structures known as phylogenetic trees. An evolutionary tree T = (V,E) represents genealogical relationships among living species (located at the leaves of the tree) and hypothetical extinct species (represented by internal nodes) by defining linkages between ancestors and descendants by means of branches.
The search for phylogenetic trees is usually formulated as an optimization problem by defining optimality criteria. In this research, we will focus on two widely-used criteria: maximum parsimony and maximum likelihood.
Inspired by the Ochkam's razor principle, maximum parsimony methods were defined to address the search for phylogenetic trees that minimize the amount of mutation events needed to explain the observed data. Therefore, parsimony analyses seek for the simplest evolutionary history of living organisms. Given a phylogenetic tree T = (V, E) inferred from a set of N sequences of M nucleotides, where u, v in V represents two nodes related by a branch (u, v) in E, we can compute the parsimony score for T as follows:
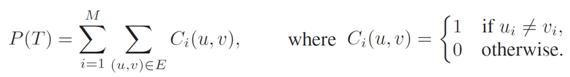
This expression requires the assignment of ancestral states to internal nodes. For this purpose, we can apply Fitch's algorithm. We can distinguish two main steps:
-
Bottom-up assignment. The initial ancestral state assignment for each node is carried out in the following:
- Terminal nodes: initialize the state set with the corresponding input sequence.
-
Internal nodes: given a node u with children v,w, we compute ancestral states Si(u) for each site i as follows:
- Si(u) = Si(v) ∩ Si(w) if (Si(v) ∩ Si(w) is not empty)
- Si(u) = Si(v) ∪ Si(w) if (Si(v) ∩ Si(w) is empty)
- Top-down labelling. Starting from the root node, we choose any state contained in Si(r) as the final state for character i (Li(r)). For each children u, we will assign Li(u) as Li(r) if Li(r) is contained in Si(u). Otherwise, we set Li(u) by choosing any state in Si(u). This process is repeated for each internal node in the topology, generating a final ancestral state assignment that minimizes the number of character changes observed.
Figure 2 shows an example of applying Fitch's algorithm to compute the parsimony score.
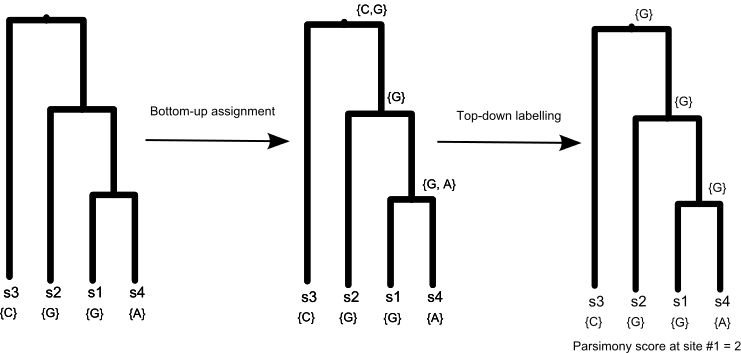
Figure 2: Parsimony computation
On the other hand, maximum likelihood methods use the likelihood statistical measurement to infer statistically reliable phylogenies. Likelihood measures the probability of observing the input data given an evolutionary hypothesis modelled by a phylogenetic tree and a model of molecular evolution. Evolutionary models provide substitution matrices that define the probability of observing mutation events at molecular level. The main purpose of likelihood-based methods is the reconstruction of the most likely evolutionary tree that explains the results observed at the input of the procedure. Those phylogenies that maximize the likelihood function will be preferred over other ones.
Given an alignment of N molecular sequences with M characters per sequence, an alphabet Λ which defines possible character states, and an evolutionary hypothesis represented by a phylogenetic tree T = (V,E) and an evolutionary model θ, the likelihood function can be expressed as follows:
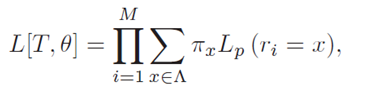
where πx is the stationary probability for the character state x, and Lp(ri = x) the partial likelihood score of the root node, conditional on observing x at position i. According to Felsenstein's pruning algorithm, the partial likelihood for an inner node u in V with descendants v,w in V can be calculated by using a recursive approach which verifies the following:
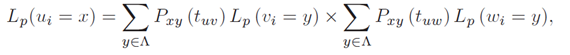
where Pxy represents the probability of observing a mutation from state x to y after a time t. Finally, the partial likelihood for a terminal node l in V is given as follows:
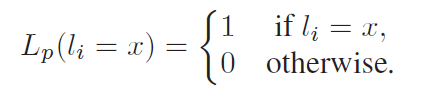
In order to make clear this formulation, we provide in Figure 3 an example of likelihood computation.

Figure 3: Likelihood computation
Given different criteria, such as parsimony and likelihood, a multiobjective approach can be useful to overcome the problems that arise when different methods provide conflicting explanations about the evolutionary history of species. The main goal to achieve is the development of efficient approaches based on metaheuristics and parallel computing to infer a set of trade-off solutions that represent good compromises among conflicting criteria.
References
- "Applying a Multiobjective Metaheuristic Inspired by Honey Bees to Phylogenetic Inference". Sergio Santander-Jiménez, Miguel A. Vega-Rodríguez. BioSystems, Volume 114, Issue 1, Elsevier Science, Oxford, England, 2013, pp. 39-55, ISSN: 0303-2647. (Impact factor = 1.472)
- "Parallel Multiobjective Metaheuristics for Inferring Phylogenies on Multicore Clusters". Sergio Santander-Jiménez, Miguel A. Vega-Rodríguez. IEEE Transactions on Parallel and Distributed Systems, Volume 26, Issue 6, IEEE Computer Society, Los Alamitos, CA, USA, 2015, pp. 1678-1692, ISSN: 1045-9219. (Impact factor = 2.170 in 2014)
- "On the Design of Shared Memory Approaches to Parallelize a Multiobjective Bee-Inspired Proposal for Phylogenetic Reconstruction". Sergio Santander-Jiménez, Miguel A. Vega-Rodríguez. Information Sciences, Volume 324, Elsevier Science, New York, NY, USA, 2015, pp. 163-185, ISSN: 0020-0255. (Impact factor = 4.038 in 2014)
- "A Hybrid Approach to Parallelize a Fast Non-Dominated Sorting Genetic Algorithm for Phylogenetic Inference". Sergio Santander-Jiménez, Miguel A. Vega-Rodríguez. Concurrency and Computation: Practice and Experience, Volume 27, Issue 3, Wiley-Blackwell, Malden, England, 2015, pp. 702-734, ISSN: 1532-0626. (Impact factor = 0.997 in 2014)
- "Performance Evaluation of Dominance-Based and Indicator-Based Multiobjective Approaches for Phylogenetic Inference". Sergio Santander-Jiménez, Miguel A. Vega-Rodríguez. Information Sciences, Volume 330, Elsevier Science, New York, NY, USA, 2016, pp. 293-314, ISSN: 0020-0255. (Impact factor = 4.038 in 2014)
